Plate Boundary Layer

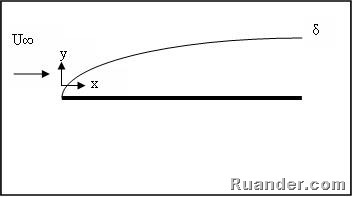
A classic fluid mechanic problem is the application of the laminar boundary layer equation to a flow over a very thin flat plate. This case was first developed by Prandtl and later solved by his student Blasius. Imagine a uniform steady flow with a velocity U∞ approaching a thin flat horizontal plate as in the figure below.

 

 

For this case the pressure gradient, dp/dx, is equal to zero. The boundary-layer equation for this flow becomes:

The boundary conditions for this flow are:
At y = 0; u = v = 0, (No Slip at the wall)
At y → ∞; u = U∞
Utilizing the definition of the stream function, ψ, and defining a similarity parameter, η as:

The partial differential equation can be transformed to an ordinary, non-linear, third order differential equation (Known as the Blasius equation). Without going into further mathematical details, the Blasius equations needs to be solved numerically (shooting method usually) to obtain the velocity profile given below:

Note that η is a function of both x and y, and thus it is sometimes referred to a stretched coordinate since it includes both the effect of changes in x and y. As η goes to infinity, the velocity becomes U∞ as it should.