Surface Wave Equation

Here is an equation that has a simple but important result, especially if you are a surfer. As a surfer, one tends to judge the waves by their size (height) and their speed. However, what is the relationship between these two parameters?To find out, let’s look at a surface wave. It is important to first notice that there are two possible frames of reference from which one could look at this problem. The first frame of reference is the one of an observer on the shore that sees the wave moving at a velocity C, while the water in front of the wave appears to be still. The second frame of reference is that of the surfer riding along with the wave that sees the water in front of the wave coming toward him at a velocity C, while the wave appears to be stationary. These two frames of reference are illustrated in the picture below.

To solve this problem it is easier to choose the surfer’s frame of reference (fixed wave frame of reference) because it provides a steady flow inertial frame of reference which simplifies the analysis significantly. Consider a control volume with boundaries right before and right after the wave, as shown in orange boundaries in the next figure. If one assumes that the shear force at the bottom surface is zero, the only forces acting on the control volume would be the hydrostatic pressure force of the fluid.

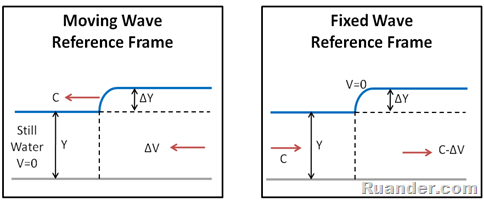
Applying the principles of conservation of mass and conservation of momentum to the control volume as follows, one can arrive at a very interesting result:

The equation boxed in red above shows that the bigger the wave height is (ΔY), the faster the wave moves (C). This equation also shows that the speed of the wave, C, increases with increasing depth, Y. Even though quite simple, the equation above has significant implications, for example the sport of surfing, and can be used to compute the speed of surface waves for different water depths and wave heights. For example for a water depth of Y=4 m and a wave height of ΔY= 1.5 m, the wave velocity is C=8 m/s.

It is important to mention that if the depth of the water, Y, is much bigger than the height of the wave, ΔY, (Y>> ΔY), then the equation becomes:

The above equation is the surface-water equivalent of fluid sound speed. Normalizing a flow velocity by the wave velocity given by the equation above gives the non-dimensional number known as Froude number which is the analog of Mach number in fluid sound speed.