Sum of Two Dice

I typically don’t play much board games. However, recently I played a game called Settlers of Catan and really enjoyed it. Besides the great company and  food, one of the many things that I enjoyed about the game was the statistics. I am talking about simple statistics that boils down to the probability of rolling numbers between 2 and 12 using 2 fair dice.  Note that when rolling two dice, there are 36 different possible combinations. This is shown in the table below:

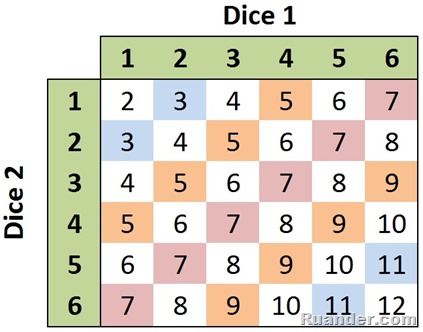
Note that in these 36 different combinations, some outcomes appear more times than others. For example, the number 7 appears 6 times in the table while the number 2 only appears only once. Therefore, there is a higher probability to roll a 7 than to roll a 2. To compute the probability of rolling a 7 one must divide the number of times 7 appears on the table by the total number of possible combinations. That is 6/36=0.167 or 16.7% chances of rolling a 7. If we do this for all possible sums, we get the following:

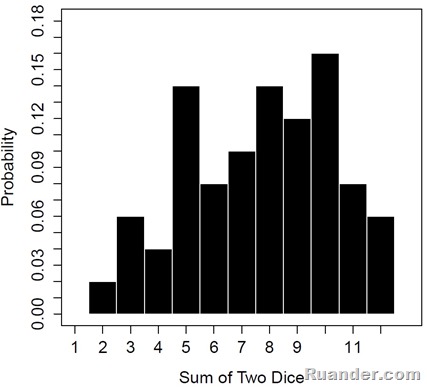
Using this information, one can plot the probability density function as shown below:

as well as the cumulative distribution function:

Ok, this all looks good. However, I would like to bring the theory into practice. I would like to roll two dice 1 million times and then compute the actual probability density function that I would get. This seems like a lot of work but fortunately, I can ask a computer to roll the dice for me to make it much quicker.  Here is what I got:

Comparing the theoretical probability density function with the one obtained numerically, I would say they are in excellent agreement. They both have triangular distribution with equivalent magnitudes.

Ok, from the information above, I would say I am definitely betting on the numbers 6, 7, and 8 to play Settlers since they have the higher probability of occurrence. Unfortunately, there aren’t 1 million dice roll during the game.  Let’s say there are about 50 dice throws during 1 game.  I will ask the computer to run 4 games. Lets see what we get:

Game 1:

Game 2:

Game 3:

Game 4:

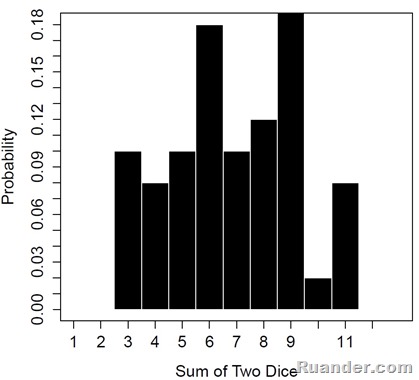
Well, it seems like 50 dice rolls is a small enough number that the probability of getting any one combination varies a lot. Maybe this is why I didn't win the game despite betting on high probability outcomes :).

By the way, here is the code that I used in the computer (written in R) to roll the dice:

#######################################################################################################################################################################################

#Created by Ruander Cardenas
#Last Updated on 6/12/2013

#Number of Throws to Simulate
N=50

#init array
Dice1 <- rep(NA, N)
Dice2 <- rep(NA, N)

Dice1 <- sample(1:6, N,replace = TRUE)
Dice2 <- sample(1:6, N,replace = TRUE)

SumDice=Dice1+Dice2

#number of bins for the histogram
bins=c(1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5,10.5,11.5,12.5)

#Plot Histogram with set color, labels, and in a way that allows to find the max count
list_histo <- hist(SumDice, breaks=bins, freq=FALSE,col="black", border="white",xlab = expression(paste("Sum of Two Dice")),ylab="Probability",main ='',xlim=c(1,13),ylim=c(0,0.18),axes=F)
axis(1, at=seq(1 , 12, by=1))
axis(2, at=seq(0 , 0.18, by=0.01))
box()

#######################################################################################################################################################################################