Monte Carlo Analysis: Right Triangle

Here is a very simple problem. Assume you want to build a right triangle of known base (10) and height (3) dimension. However, the sigma tolerance of these dimensions are 1% of its value. Your goal is to find the variability that you will obtain for the dimension of the hypotenuse and the largest of the two complementary angles. It is straight forward to do some simple math to figure out the nominal value for the two variables of interest. This is shown in the figure below:

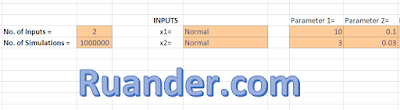
Note that the variables of interest are not linear with respect to the known variables. Therefore, it is not possible to simply add the variances of the two known dimensions. It is possible to use the principles of propagation of uncertainty to propagate the known variation through the non-linear equations. This exercise will be left to the reader. Here, I will show how you can quickly use my Excel Monte Carlo Workbook to solve this problem. First, download the free version of this workbook or if you wish, you can also purchase the non free version here.  Set up the problem with 2 input variables of normal distribution with the given mean and sigma values. The inputs will look like this: 

After setting up the problem, simply  run a large enough number of simulations by entering the number of simulations in cell F6 and then click the "2. Simulate" bottom. I recommend running at least 500K simulations. For this example, I will run 1M simulations. After the simulation is completed, just type in the formula to compute the hypotenuse and the angle as shown in the first figure above. Drag this equation down for all the simulations performed. 

Finally, simply compute the average and standard deviation for the variables of interest. The results are the following:

As mentioned earlier, if you follow the principles of uncertainty propagation using partial derivatives, you will arrive at this same result (Rule No. 5 here). This is shown in the table above under the Analytical column. Using the Monte Carlo Excel you can also visualize the distribution of these two variables.

I hope this example is useful to help identify other relevant applications where a Monte Carlo Analysis can help you understand variation of non-linear problems.